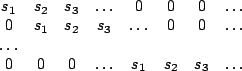Next: Computational efficiency
Up: Estimating camera response function
Previous: Estimating camera response function
We can make an inference that the true 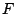 is probably smooth, and,
as mentioned previously,
is probably smooth, and,
as mentioned previously, 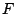 must be semimonotonic.
must be semimonotonic.
Thus the estimate of 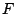 can be constrained in both smoothness and
monotonicity. A smoothness constraint may be formulated
by appending
can be constrained in both smoothness and
monotonicity. A smoothness constraint may be formulated
by appending 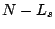 extra rows to
extra rows to 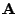 and the same
number of extra zeros to the end of
and the same
number of extra zeros to the end of 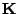 ,
where
,
where 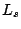 is the length of the appropriate
smoothness filter,
is the length of the appropriate
smoothness filter, 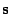 , and then
solving (12).
The extra rows appended to
, and then
solving (12).
The extra rows appended to 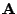 are constructed as follows:
Let
are constructed as follows:
Let
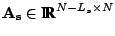 denote the portion appended to
denote the portion appended to 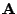 ,
and create
,
and create
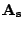 as a toeplitz matrix in which the first
as a toeplitz matrix in which the first 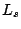 elements
of the first row are the filter coefficients, and the remaining
rows are appropriately shifted versions of the coefficients:
A_s =
[
elements
of the first row are the filter coefficients, and the remaining
rows are appropriately shifted versions of the coefficients:
A_s =
[
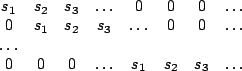
]
In order to achieve smoothness, the filter needs to be a
highpass filter.
(The intuition for this comes from the fact that by ``looking''
at the function through a highpass filter,
this makes it ``expensive'' for the curve
to have high frequency (non-smoothness) content since the
right hand side vector for this portion of the matrix equations is zero.)
The simplest filter is a three-tap filter
![$\lambda [1, -2, 1]$](img72.gif) for which
the effect of appending the corresponding
for which
the effect of appending the corresponding
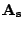 to
to 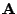 is to impose a penalty for
nonzero second derivatives (inflection) of the curve
is to impose a penalty for
nonzero second derivatives (inflection) of the curve 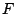 .
The amplitude,
.
The amplitude, 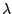 , of the filter, determines
how heavily the smoothness constraint is weighted.
Additionally, a monotonicity constraint may be imposed using
Quadratic Programming (QP).
, of the filter, determines
how heavily the smoothness constraint is weighted.
Additionally, a monotonicity constraint may be imposed using
Quadratic Programming (QP).
Examples of determining the response function, 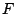 , from two differently
exposed images, are shown in Fig 2(a).
, from two differently
exposed images, are shown in Fig 2(a).
Figure 2:
(a) Response functions estimated from the data for no smoothing
(solid line), smoothing with 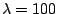 (dotted line),
and smoothing with
(dotted line),
and smoothing with 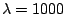 (dotted line).
(b) Derivatives of the response functions make the effects of
smoothing more evident. The derivative of the response function
is called the certainty function, because it shows the sensitivity
of pixel integer output as a function of changes in
light [7].
Slight ripple in the response function becomes magnified
and visible as periodicity components in these certainty functions.
Note how the harmonic contributions have a period of
(dotted line).
(b) Derivatives of the response functions make the effects of
smoothing more evident. The derivative of the response function
is called the certainty function, because it shows the sensitivity
of pixel integer output as a function of changes in
light [7].
Slight ripple in the response function becomes magnified
and visible as periodicity components in these certainty functions.
Note how the harmonic contributions have a period of 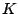 (normalized to stepsize
(normalized to stepsize 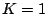 in this plot).
in this plot).
 |
The rippling is particularly evident when we consider the derivatives
of the response functions as shown in Fig 2(b).



Next: Computational efficiency
Up: Estimating camera response function
Previous: Estimating camera response function
Steve Mann
2002-05-25